Martian Dice Statistical Analysis

About The Game

Martian Dice is a fun little dice game with more strategy and player choice than a lot of similar games, like Zombie Dice. You’re playing the alien invaders, equipped with death rays, and are out to abduct as many earthlings as possible. The humans are equipped with tanks to defend against you.

The game has thirteen dice, each of which has on it’s six sides: Tank, 2 x Death Ray, Human , Chicken, Cow. For the rest of this post, to make the dice representation a bit easier, I’ll represent a dice roll by TTA:TTRRRAAACB (A: Human, B:Chicken, C:Cow). The dice to the left of the colon have been taken in a previous turn, the dice to the right are freshly rolled.

The rules of the game are relatively simple:

1. Roll all the available dice.
2. Set aside all tanks, adding them to any set aside previously.
3. From the remaining dice, choose one type. Humans, chickens, or cows can not be chosen if they have been taken previously. Death Rays can always be chosen.
4. If any dice remain, you can return to step one and reroll, or choose to stop playing and proceed to scoring. If you were unable to take any dice, or no dice remain, proceed to scoring.
5. Score. If there are more tanks than death rays, then the score for the turn is zero. Otherwise, each human, chicken, or cow dice is worth one point. If you grabbed at least one of all three earthling types, then you get an additional three points.

An example turn (taken from the instructions):

Motivation

I almost always bring along this game when I go camping. It’s fast to teach to new players, it’s easily washable, and has more player decisions than a normal dice game. I was losing quite a lot of games (I tend to push my luck more than I should) and realized I didn’t have a good intuitive grasp on the impact my decisions would make in the game. So, I decided to investigate some of the in-game choices that are hardest for me to make, and at the same time try to create a perfect computer player that would understand all the probabilities and, at each decision tree, would make the choice that would maximize his score.

Probability to Survive a Reroll

The first thing is to look at the probabilities of different dice rolls. The order of the dice is not important, only the number of each dice that is rolled. So, I needed to determine both the total number of different dice combinations for a given number of free dice (N), and the probability that a particular combination will be rolled. These are given by the following two equations, and good explanation for which can be found here:

One thing I wanted to determine was the probability, for any given combination of dice, that a reroll would result in a loss. The player choice in this game makes any kind of probability calculation difficult, so I’m assuming for all the following work that the player always makes the best choice (in this case the choice that maximizes his survival probability). This probability depends only on the number of excess tanks (ΔT), how many types of earthlings have already been taken (E), and the number of free dice remaining (N).

In the simplest case, TTTTRRRRAAAA:?, where there is only one free dice, as many death rays as tanks, and only one type of earthling taken, we only need to examine one die to determine the probability of winning. The dice has five options, the probability of rolling a death ray is $\frac{1}{3}$, and $\frac{1}{6}$ for all others. The only roll that would result in a loss is a tank, so the probability of surviving in this case is $\frac{5}{6}$ or 0.83. In the equation below, the right column is all the combinations with the same survival probability, the middle is the probability of rolling one of the listed combinations, and the left is the survival probability for the given combination.

A more complicated example, TTTTTRRRRA:???, takes a bit more work to calculate. In order to win, the player must get at least a single R. And, since there are multiple dice, rerolls have to be taken into consideration. For this example, there are four different cases to be considered: lose, win, one dice to reroll, two dice to reroll. In both of the reroll cases, a single death ray and no tanks would considered a successful reroll. Here there are 35 possible combinations, and the probability of rolling a particular combination varies. The total probability is then given by, for each combination, summing the probability of the combination times the probability of surviving that combination. Ihe survival probability for this example is 0.614.

The previous case is about as far out as I was willing to go with hand calculation, but I was willing to spend the time to write a perl program to recursively calculate everything for me. For any given combination of dice, it will follow steps very similar to the above examples. It will calculate the probability of occurrence for each combination of N dice. Then, for each of those combinations, it will calculate the probability of losing. Whenever presented with a choice (EG: Taking death rays or chickens), it calculates the probabilities for each of the different valid choices, and then takes the one that maximizes the value. Finally, it determines the actual probability of survival using the equations in the previous section. I matched the results of the program to the values I calculated by hand, and always found them to match exactly.

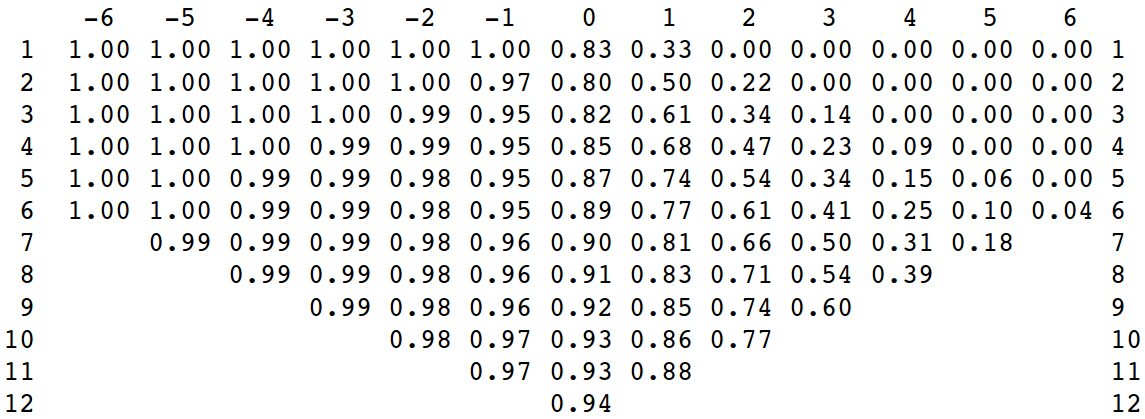
The following table shows the probability that a reroll will result in a win. It isn’t taking score into consideration, it’s only looking at whether there are more tanks than death rays at the end of the game. So, it would consider a game of TTRR a win, even though the score is zero. The plot is excess tanks (T-R) VS number of free dice (N).

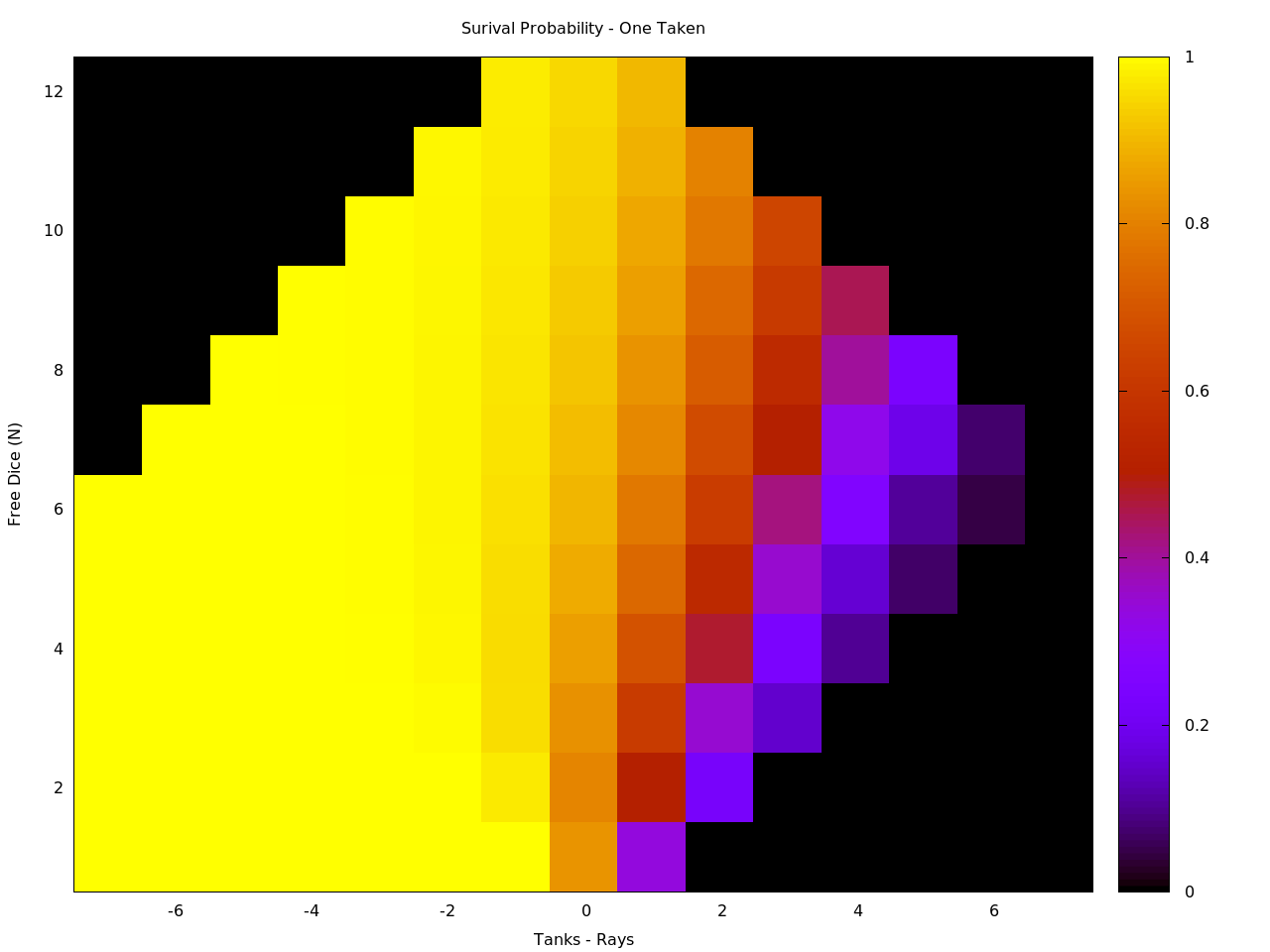
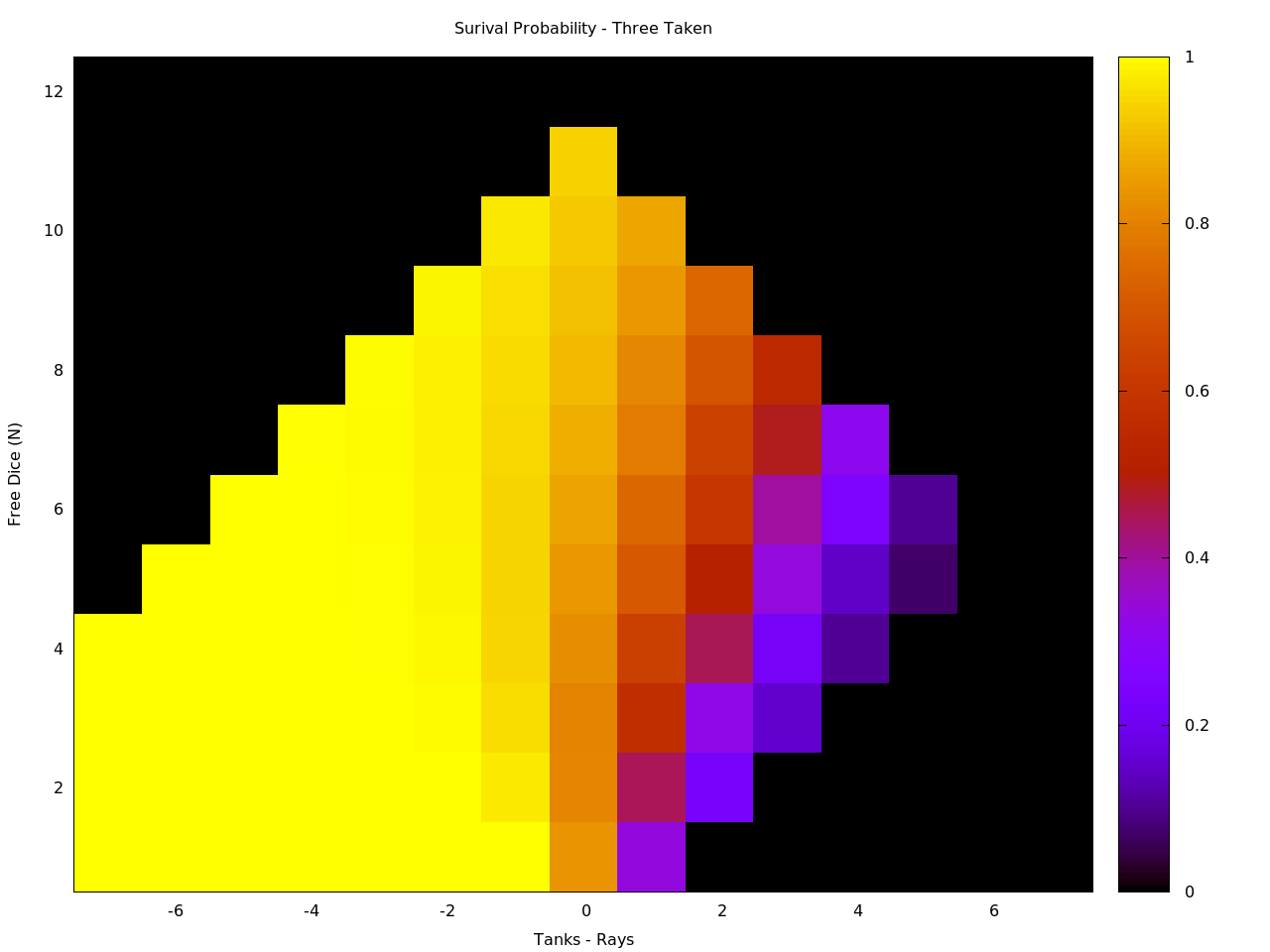
The rules state that a single earthling type can never be taken more than once per game. To see how this would affect the survival probability, I calculated it for the case of having taken one, two, and again for all three earthling types. I was surprised to find that the number already taken before rolling had very little effect, only making a noticeable difference in the cases with very few free dice. Below are heatmaps done, on the same scales, for both one and three earthlings already taken.

Survival probability. E=1 and E=3 (number of earthlings taken before rerolling).

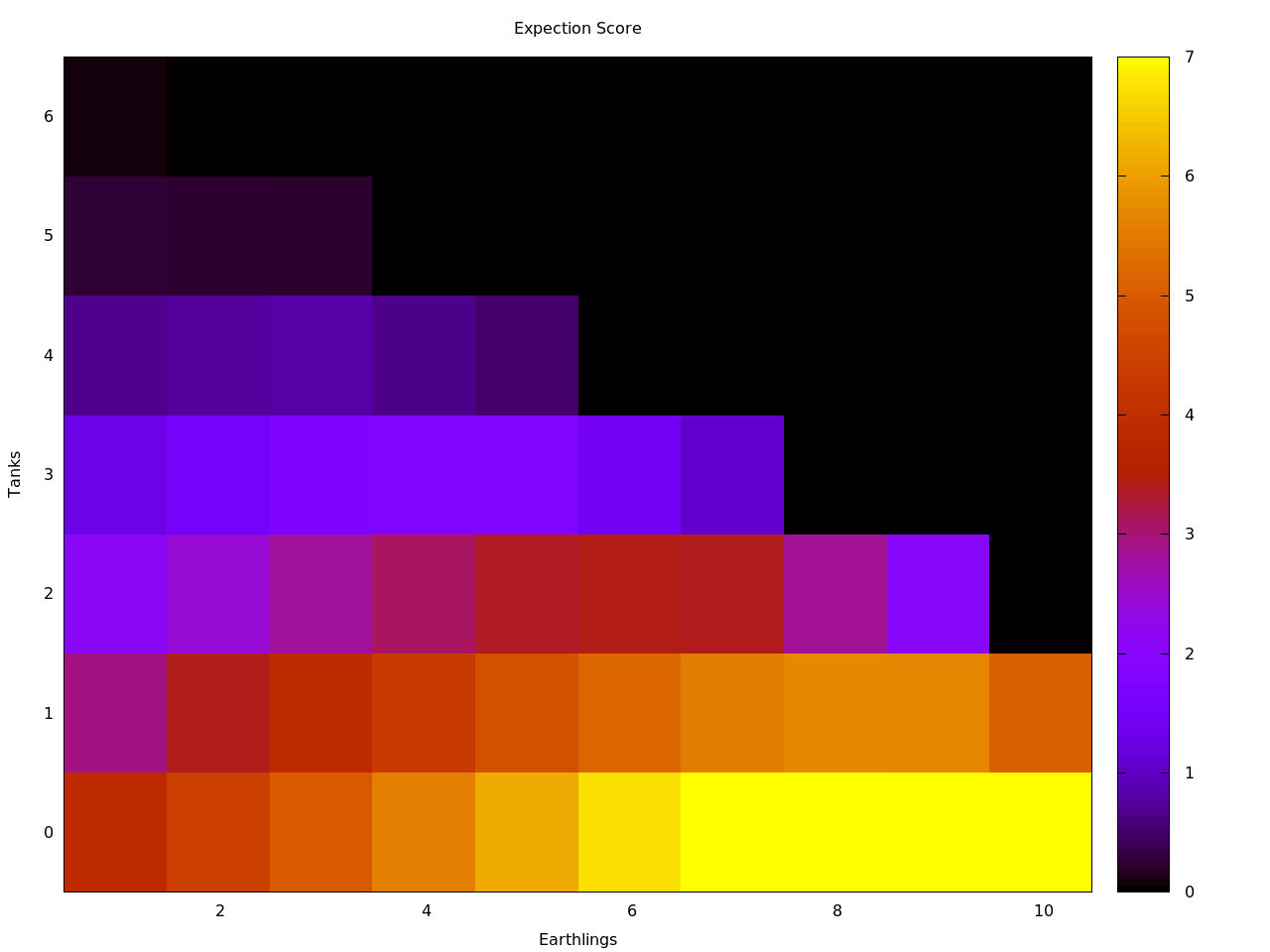
Expectation Score

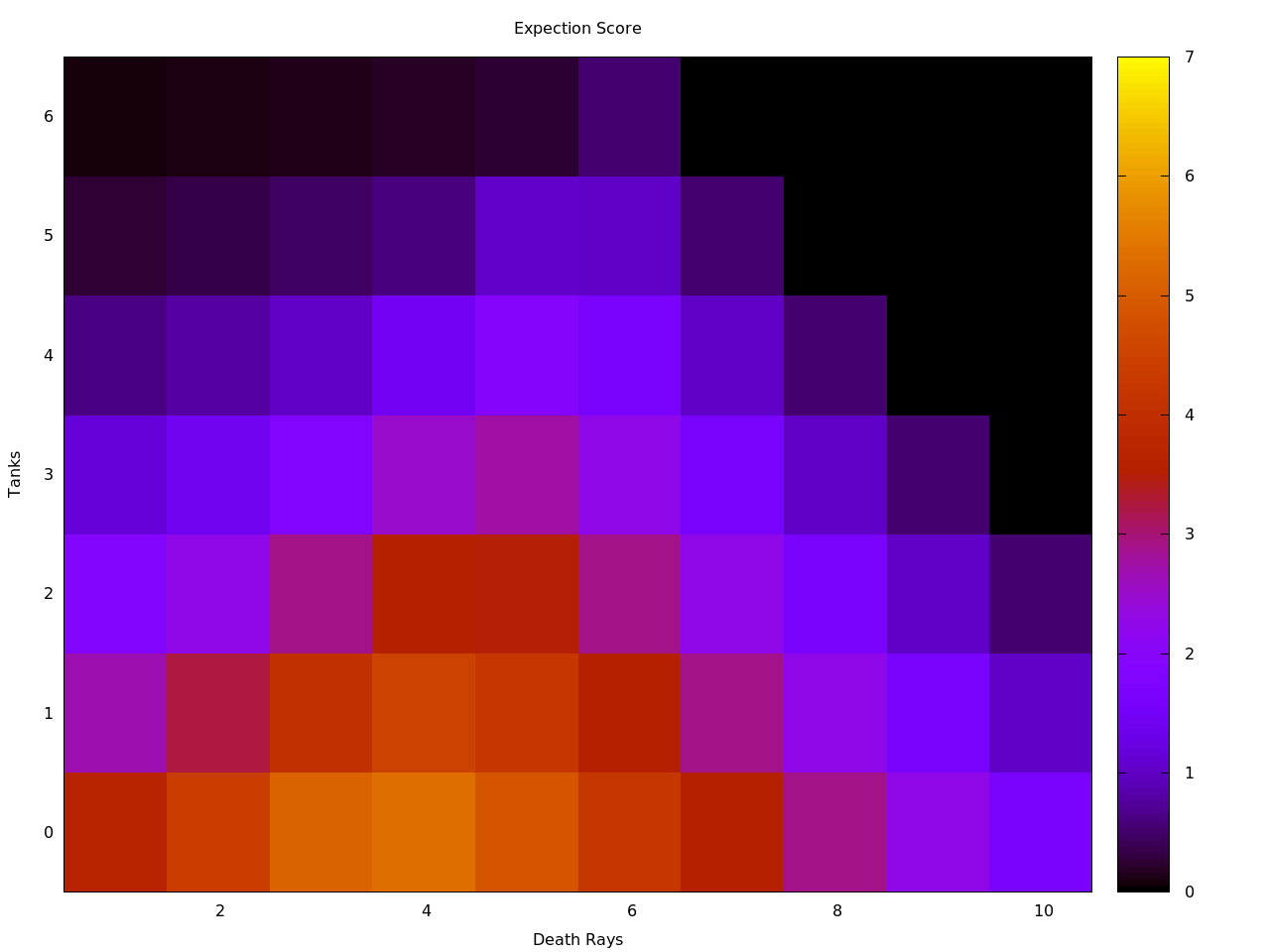
My next goal was to try to figure out the expectation score for any given dice distribution. In other words, if a set combination of dice was perfectly played an infinite number of times, the average of all those games would be the expectation score. The process to calculate it is almost identical to the previous section. As before, I set the computer to calculate out the expectation scores for all possible dice combinations and then compared it’s results to a small selection of hand calculated results.

Looking at the same case used in the earlier example, TTTTRRRRAAAA:?, where there is only one free dice, as many death rays as tanks, and only one type of earthling taken, we only need to examine one die to determine the expectation score. There are three possible cases to consider: losing, returning the same score, or returning an increased score. The expectation score in this case is 3.67, and since the current score is 4, a reroll would most likely result in a lower score.

The expectation score for a game of Martian Dice is 3.11.

First Roll

I wanted to answer the the question, “which dice do I take on the very first roll?” I have always found this to be the most difficult of the game. Frequently I’ll roll a large number of death rays and no tanks, or a few tanks and a large number of earthlings. In the death ray situation, I never could figure out whether it’s best to take the death rays as a buffer against future tanks, or pass on them with the hope of getting a more valuable roll later.

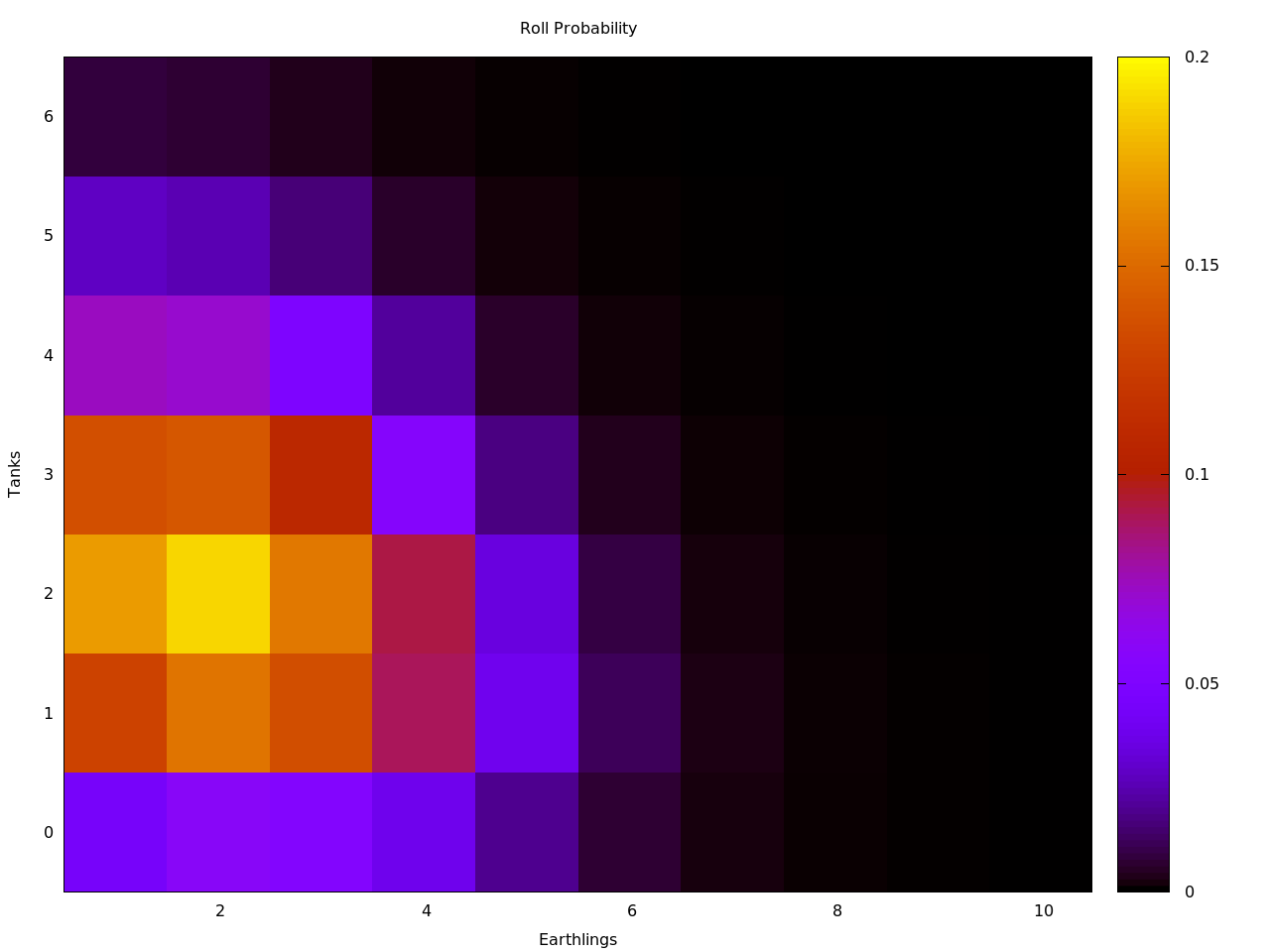
The following tables are the calculated expectation scores for a first roll, where no dice have been taken. Plotted is the number of tanks rolled VS the number of death rays or earthlings taken, followed by the probabilty for the same plots.

Expectation for a first roll. Rolled Tanks VS Death Rays or Earthlings. I've capped the color scale at 7, so for the A plot 7-12 are all the same shade of yellow.

Probabilty for the first roll. The plot has the same axis as the above.

A complete list of all 2380 first roll combinations, along with the various expectation scores, is located here.

Perfect Player

Next I set up a computer player to play the game. It would keep rolling as long as it’s current score was less than the expectation score. Whenever a choice needed to be made, it would consider all the options and pick the one that maximizes it’s score. An example of this process is below.

ROLLED:         T=1   R=4   A=1   B=5   C=2 
SCORES:               R=4.5 A=2.9 B=4.8 C=3.4
  Taking B with score 4.77
LOOP:     N=7   T=1   R=0   A=0   B=5   C=0
-
ROLLED:         T=0   R=3   A=2   B=2   C=0 
SCORES:               R=7.2 A=5.7 B=0.0 C=0.0
  Taking R with score 7.16
LOOP:     N=4   T=1   R=3   A=0   B=5   C=0
-
ROLLED:         T=0   R=3   A=1   B=0   C=0 
SCORES:               R=5.3 A=8.0 B=0.0 C=0.0
  Taking A with score 8.04
LOOP:     N=3   T=1   R=3   A=1   B=5   C=0
-
ROLLED:         T=0   R=0   A=0   B=2   C=1 
SCORES:               R=0.0 A=0.0 B=0.0 C=10.0
  Taking C with score 10
LOOP:     N=2   T=1   R=3   A=1   B=5   C=1
-
FINSIHED:       T=1   R=3   A=1   B=5   C=1
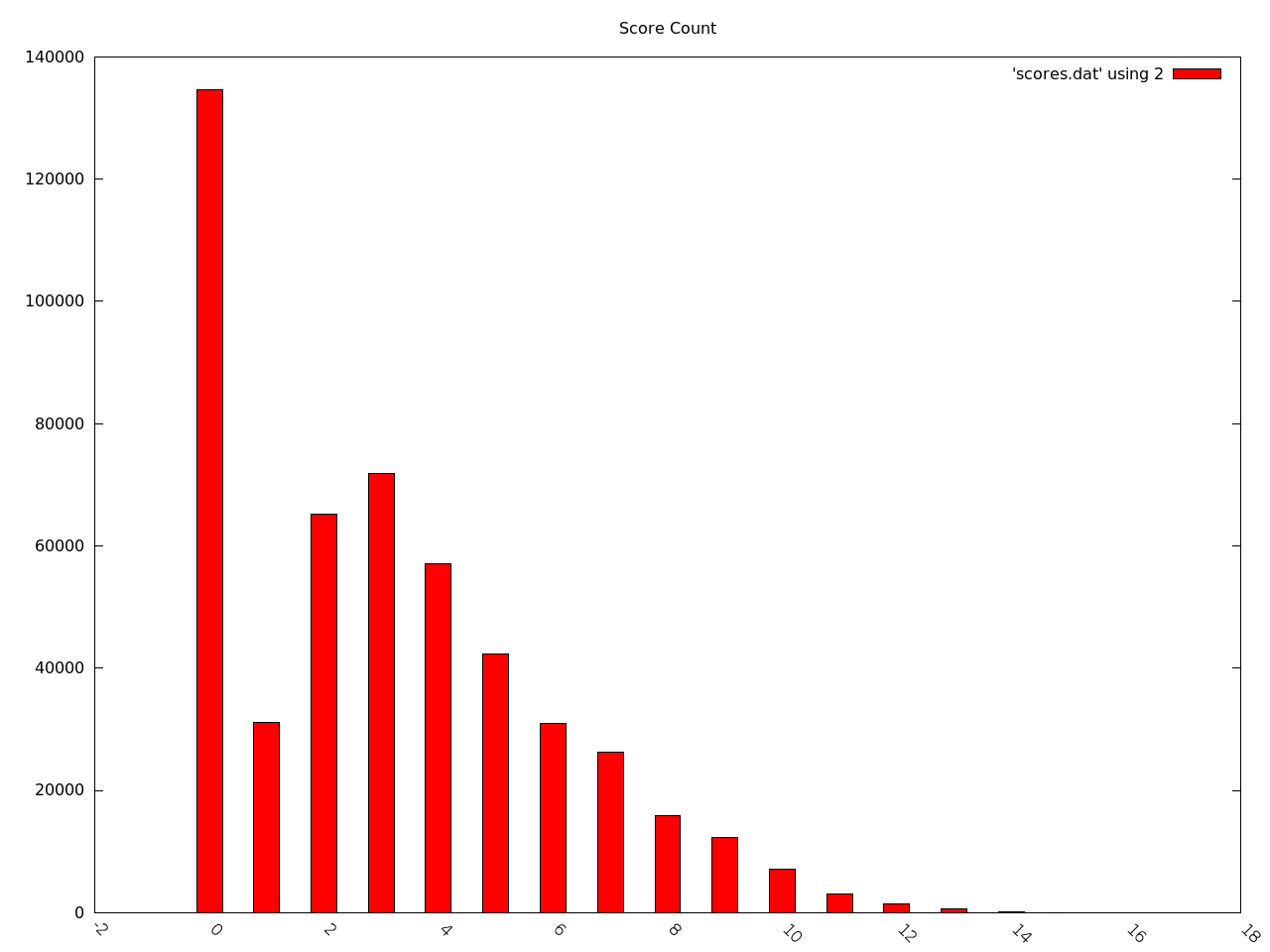
FINAL SCORE: 10

I let the program run for a a million iterations, and I came up with some numbers for the perfect player. The average score for a game is the same as the expection score, 3.11. 27% of games will end in a loss, and the average score for the winning games was 4.25. A histogram showing the score breakdown for one million games is below.

Interactive Game

I created an interactive version of the game as well. In addition to playing traditionally, it’ll report the expectation scores for each of the different rolls as you play. So, think of it as a Martian Dice trainer, just in case you’re planning to go pro.

• ← Previous Post
• Next Post →